Escape Velocity and Space Exploration

Posted on February 9, 2024 by katie shapiro
Escape velocity required to escape Earth’s orbit: Collegedunia Team

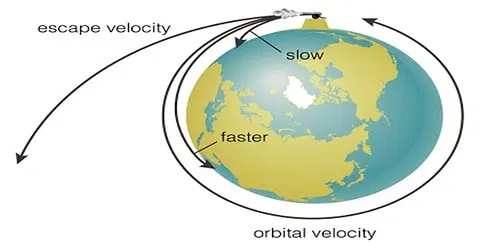
In our generation, space exploration has been an extremely valuable way to learn more about our solar system and our galaxy, the Milky Way. It is astounding that humans have been able to set foot on the moon, and that astronomical research centers have sent probes to a variety of astronomical objects within our galaxy, including planets. However, how is it possible that we are able to have objects, such as rockets, leave earth to explore the unknown within space? One main component of this is escape velocity, which was revealed by Issac Newton in the 1700’s. This is the speed that is required for any object to leave or escape a gravitational pull. One common example of this, is Earth’s escape velocity which is approximately 11.2 km/s, which is very fast! In fact, the escape velocity is about 34 times the speed of sound. The escape velocity was founded upon the important principle of the conservation of energy, in which energy cannot be created or destroyed. The equation for escape velocity implies that the final kinetic and potential energy are equal to zero due to an infinite distance. So the initial kinetic and potential energy are set equal to zero and the final equation is ve = SqrRt (2GM/R). Additionally, the escape velocity depends on where the object is in relation to the planet. One example, is that near the equator in the east, the escape velocity is less than the escape velocity in the equator in the west. However, a more commonly known example is that the escape velocity depends on the altitude of where the object is in relation to the planet. For example, if it is further away from the surface, then the escape velocity is much less, than if the object was at the surface because the distance is greater. This is seen in the equation listed above because the square root of R (distance) is inversely related to escape velocity. This understanding is important when applied to rockets escaping earth. When they are launched they will orbit Earth near the surface with an orbital velocity. In this orbit they have to reach a certain velocity in order to escape the gravitational pull that was initially holding the rocket to earth. Once the escape velocity is acquired, the rocket can then escape Earth’s gravitational pull, regardless of its mass, and reach its assigned destination. It’s crazy to think that without Issac Newton’s outstanding work on gravity and his initial finding of escape velocity, we would not have had the outstanding space exploration that we have today!

, , ,
, , , ,
Posted in Class, Physics, Space Travel, Universe | Tagged , , , , , , , , | Comments Off on Escape Velocity and Space Exploration

Historical Astronomers in Context

Posted on February 8, 2024 by Jonas Kobza

Nicolaus Copernicus – 2/19/1473 – 5/24/1543

Nicolaus Copernicus the first in the modern era (C.E) to develop a model of the universe with the sun at its center, rather than the earth. His work sparked the Copernican Revolution, a paradigm shift which paved the way for the works of Kepler, Galileo, Newton, and others. Copernicus was also the first to propose that the day/night cycle of earth was caused by a rotation on its axis, rather than the earth rotating around the sun. Copernicus’ model paved the way for future astronomers to unlock more about our place in the universe.

Events in Copernicus’ lifetime

Columbus discovers the New World (1492) – This discovery sparked European colonization of the Americas, and the exchange of goods and ideas between Europe and the New World. It also caused extreme violence and disease against the indigenous peoples. 

Protestantism Reformation was started by Martin Luther (1517) – The protestant reformation was a religious movement started in the early 16th century. It had many social and cultural consequences, such as challenging the authority of the Catholic Church and Pope. It also helped to promote increased education and critical thinking through movements such as skepticism.  

Historical Figure Alive 

Niccolò Machiavelli (1469-1527) – Considered the creator of modern political science, Machiavelli’s book “The Prince” is guide for political leaders to better control, lead, and win support over their people.

Reflection

Copernicus lived throughout the Renaissance, a time when middle ages/dark ages ideals of philosophy, science, and art, were challenged. It is no coincidence that Copernicus’ theory of heliocentricity was published after the Protestant Reformation began. This is because Martin Luther, and other reformers such as John Calvin challenged previous ideals such as church and papal infallibility, or the idea that the Pope and Church are without error in their decisions and teachings. This laid the groundwork for Copernicus, and later Galileo and Kepler to challenge the church with their scientific research. Without the movements of the Renaissance and Protestant Reformation, they may never have pursued astronomy and science, and never challenged previous beliefs.

Posted in Historical | Tagged , , | Comments Off on Historical Astronomers in Context

Historical Astronomers in Context

Posted on February 6, 2024 by Alyssa Ballard

I chose the astronomer Johannes Kepler who was born on December 27th, 1571 in Germany and died on November 15th, 1630 (age 58) in Germany. In the timeframe that Kepler was alive, Shakespeare died, the thirty-year war began, and the protestants began their revolt against the Catholics. Overall this assignment helped me realize more of what people were doing back then, and why so many people were astronomers at that time. There were so many artistic and historic things going on, that they all kind of blended together to make one whole section of time; as in the Renaissance era. It also helped me understand the time period in general a little bit better, as far as what was going on in history at the time as all of these astronomers were finding gravity and the solar system.

Posted in Historical | Tagged , , | Comments Off on Historical Astronomers in Context

Historical Astronomers in Context

Posted on February 6, 2024 by Leni Ertel

Johannes Kepler (1571-1630) was important to astronomy because he discovered that orbits are not perfectly circular, but move in ellipses. He is credited with three laws that are still heavily used in the study of astronomy. Kepler’s first law is: “The orbit of each planet about the sun is an ellipse with the sun at one focus.” Kepler’s second law is: “A planet moves faster in the part of its orbit nearer the sun and slower when further from the sun, sweeping out equal areas in equal times.” Kepler’s third law is: “More distant planets orbit the sun at slower average speeds, obeying the precise mathematical relationship p^2 = a^3.” (Bennett et al., 65-66). 

During Kepler’s lifetime, Britain became the rulers of the Atlantic Ocean. In 1588, Britain defeated Spain’s Armada, leading to Britain becoming a world-class power (History.com). Also during Kepler’s lifetime, Shakespeare began writing his plays. It is estimated that Shakespeare’s first play was written between 1589 and 1991 (Folger Shakespeare Library). Shakespeare took the theatre world, and the general population, by storm with his accessible, entertaining, and emotional plays. Shakespeare lived during the same period as Kepler, being born on April 26, 1564, and dying on April 23, 1616. He was revolutionary in literature and performance, and completely shifted the landscape of modern entertainment (Folger Shakespeare Library).

It is interesting to get more historical context on what was happening in the world while these major astronomical revelations were being discovered. This time period was huge in terms of shifting power dynamics and scientific revolutions. Kepler was just one person during a period where many people were making huge discoveries and observations about every aspect of our world. It made me realize that this period of time is importantly relevant and instrumental in informing us of the progress we have made, and how we can look back in time to these hugely influential people and learn from their creativity, intelligence, and vigor. 

Posted in Historical | Tagged , , | Comments Off on Historical Astronomers in Context

Historical Astronomers in Context

Posted on February 6, 2024 by Ayden Harris
  1. Isaac Newton (B. December 25, 1642 D. March 20, 1727) was important because he was one of the first people to accurately describe mathematically how planetary motion works. He was able to begin to mathematically describe how gravity works and especially how it relates to mass on a massive planetary scale.
  2. When Newton was at Trinity college, they had to close due to the Bubonic Plague. It killed a quarter of London’s population. The English Civil War was also occurring when he was born. They were between the Royalists and the Parliamentarians of England.
    1. Antonie Van Leeuwenhoek was a Dutch microscopist that discovered bacteria and protozoa which helped create modern day bacteriology.
  3. During the 1600’s the scientific revolution was well underway. Whether it is Spinoza making new philosophies, Newton or Galileo making breakthroughs in astronomy and physics, or Antonie Van Leeuwenhoek in biology. The foundations of what we use today were just being laid during this time period.
Posted in Historical | Tagged , , | Comments Off on Historical Astronomers in Context

Historical Astronomers in Context

Posted on February 6, 2024 by Miguel Beristain

Johannes Kepler (Nov. 27, 1571- Nov. 15, 1630) was a German scientist and early astronomer. He was responsible for discovering three major laws of planetary motion: 1. Planets orbit the sun in an elliptical movement; 2. The area law; 3. The harmonic law. He also modified Copernicus’ Sun-centered system to a dynamic universe approach, where the Sun is active in shifting how the planets orbit around it. Much like many scientists during his time, Kepler was well-versed in many fields, including physics, mathematics, philosophy, and theology. He used the knowledge from these fields to further his understanding of the early days of astronomy.

Kepler lived through many important global events. In 1588 the Spanish Armada was defeated by the English. King Phillip II of Spain ordered the armada to aid in the planned invasion of England, but before the invasion could begin, the armada was attacked by British ships and forced away. This decisive military victory was a massive blow to what was then thought of as the greatest naval military force in the world and started the decline in Spanish military power. Additionally, in 1611 the King James Version of the Bible is published, becoming one of the most culturally important English books. The version to this day remains the preferred translation of protestant Christian groups and religious movements.

Another important and influential person who lived at the same time as Kepler was René Descartes (March 31, 1596-Feb 11, 1650). Descartes was a revolutionary figure in modern philosophy and science. In terms of philosophy, he laid the groundwork for rationalism (in opposition to empiricism), increased the importance and attention of epistemology, and famously made the groundbreaking philosophical statement “cogito ergo sum.”

Doing this research really helped me understand the (Western) astronomical timeline and put into perspective how exponentially things have changed over the 20th and 21st centuries compared to the 16th and 17th centuries. With our current technology we have abilities that past astronomers could only dream of. Not only have we sent people to space, but we are able to see the far reaches of the universe through telescopes like the Hubble and James Webb. We’ve been able to advance astronomical knowledge far past what our predecessors thought possible, but they still laid the groundwork that led to these discoveries today.

Posted in Historical | Tagged , , , | Comments Off on Historical Astronomers in Context

Historical Astronomers in Context

Posted on February 6, 2024 by Garrett

TYCHO BRAHE (1546-1601):

Tycho Brahe is most famous for making the best observations of stars and planets in his era. He did this at a time without a telescope so he provided the most accurate empirical data of celestial bodies at the time. His documentation of  planetary positions helped lead Johannes Kepler to create his laws of planetary motion. Brahe also held a geo-heliocentric view of the universe.

ELIZABETH I:

In 1558 Elizabeth I became queen. This marked the start of the Elizabethan Age, a period known for its positive changes in England. Elizabeth I helped create a more peaceful and united England especially through the resolution of religious conflicts. By the end of her rule Elizabeth I had left England a much more powerful and wealthy country.

THE SPANISH ARMADA:

In 1588 Spain sent a fleet to invade England. This fleet is known as the Spanish Armada. The invasion failed when the english navy, with better tactics and faster ships, defeated them. This was a very important event as it marked a turning point for military power in Europe, shifting the needle towards England.

WILLIAM SHAKESPEARE (1564-1616):

Shakespeare is, if not the best, the most famous writer in the English language. His works continue to profoundly influence English literature and drama. His plays explored fundamental aspects of humanity and its desires which have helped his works remain relevant throughout the centuries.

MY REFLECTION:

Tycho Brahe existed at a time when there were major shifts of power and culture in Europe. It also seems to me that Brahe was responsible for a mirrored shift in the quality of astronomy. His findings, without the telescope, were revolutionary for the time and inspired many of the foundational astronomical concepts used today. I also find it fascinating how this is reflected in Shakespeare’s work. Shakespeare frequently uses imagery related to astronomy and the night sky. I immediately thought of the line from Hamlet

“Doubt thou the stars are fire;

  Doubt that the sun doth move;

  Doubt truth to be a liar;

  But never doubt I love.”

These are literal references to astronomical theories. This is not only a beautiful use of celestial imagery, but also indicative of the era’s shift towards a more scientific understanding of space and the cosmos. Examples like this serve as a reminder of how art and science are often more connected than we think.

Posted in Historical | Tagged , , | Comments Off on Historical Astronomers in Context

Historical astronomers in context

Posted on February 6, 2024 by Angela Harris

Isaac Newton: Isaac Newton was born in December 1642 and died in March 1727. Newton made important contributions to the study of astronomy. One of Newton’s first accomplishments was the invention of integral calculus, which was an important foundation of mathematics for his astronomical discoveries. Newton’s experiments with prisms and sunlight led to the discovery of the visible light spectrum. He is also credited with inventing the reflecting telescope. One of Newton’s most notable contributions to astronomy is his three Laws of Morion which outlite his theories about gravity. 

The English Civil War (1642-1651): The English Civil War was one major historical event during Newton’s lifetime. The war was a series of conflicts between the loyalists to parliament and loyalists to the King. The war led to the execution of King Charles I in 1649 and the establishment of the Commonwealth.

The Great Fire of London (1666): Another significant event during Newton’s lifetime was the Great Fire of London in 1666. The fire burned nearly the entire city of London. The reconstruction of London after the fire greatly impacted architecture and urban planning.

John Locke (1632-1704): John Locke is a highly regarded English physician and philosopher who made important contributions to the Enlightenment. Locke is well known for his theories about liberalism which had a lasting impact on government today.

Reflection: I enjoyed this assignment because it reminded me of the Enlightenment era. I tend to think of historical events and scientific inventions as purely independent of each other so this homework helped me challenge that. It was interesting to see how Newton’s lifetime overlapped with events like the English Civil War and the Great London Fire because it provided historical and cultural context for his contributions. Learning about Newton’s discoveries in the context of this period also put into perspective the influence that the Enlightenment had on modern times.

, ,
Posted in Historical | Tagged , , | Comments Off on Historical astronomers in context

HISTORICAL ASTRONOMERS IN CONTEXT

Posted on February 6, 2024 by Ethan Popper

Galileo

Ethan Popper

Dr. Grundstrom

The Solar System

04 February 2024

Historical Figures in Context

  1. Historical Figure: Galileo Galilei – February 15, 1564, – January 8, 1642

  1. Galileo was one of the first people to use a telescope to observe the skies. In 1609, he improved upon existing designs to make his own telescope with about 3x magnification, eventually reaching up to 30x magnification. He discovered, using a homemade telescope, four moons orbiting the planet Jupiter. 
    1. Pilgrims from England arrive at Plymouth, Massachusetts, on the Mayflower which notably becomes the embodiment of the American holiday, Thanksgiving. 
    2. The Taj Mahal starts getting built in India
  3. Discovering that legendary mathematicians like Kepler, Galileo, and Brahe were born within just decades of each other makes me realize how coincidental things can be. This closeness in timing makes me wonder if we’re currently living through an era that future generations will look back on as the birth period of the next great mathematicians and scientists. This is because of the internet — it has revolutionized our lives in countless ways, connecting ideas and people across the globe. This digital age could very well be nurturing the minds that will shape the future of science and mathematics. It’s a thrilling time to be alive.

Works cited: 

Machamer, Peter, and David Marshall Miller. “Galileo Galilei.” Stanford Encyclopedia of Philosophy, Stanford University, 4 June 2021, plato.stanford.edu/entries/galileo/. 

Holyoke, Michael, et al. “Home.” Famous Scientists, http://www.famousscientists.org/galileo-galilei/. Accessed 6 Feb. 2024. 

“The Mayflower Story.” Mayflower, http://www.mayflower400uk.org/education/the-mayflower-story/. Accessed 6 Feb. 2024.

Centre, UNESCO World Heritage. “Taj Mahal.” UNESCO World Heritage Centre, whc.unesco.org/en/list/252/#:~:text=An%20immense%20mausoleum%20of%20white,masterpieces%20of%20the%20world’s%20heritage. Accessed 6 Feb. 2024.

HISTORICAL ASTRONOMERS IN CONTEXT

HISTORICAL ASTRONOMERS IN CONTEXT

Posted in Historical | Tagged , , | Comments Off on HISTORICAL ASTRONOMERS IN CONTEXT

Historical Astronomers in Context

Posted on February 6, 2024 by Robert Navarro

Johhanes Kepler was important to astronomy for many reasons, the major reason was for his 3 laws of planetary motion. One of them was that the planets orbit elliptical around the sun. Another is the square of the orbital period of a planet being proportional to the cube of the semi-major axis of orbit. (Link)

A)(Link) In the year 1577 the first clock with a minute hand was made and developed by Jost Burgi,who was a Swiss clockmaker. In 1593 Italy, Galileo developed the first thermometer.(Link)

Toyotomi Hideyoshi was born 1536, Japan and died Sept. 18, 1598. Toyotomi Hideyoshi was the feudal lord of Japan was the person that unified it together to create what it is now.(Link)

This was actually quite interesting as not only did we know the time periods the major astronomers lived from but also what was going on during that time. It also showed how long it took for new ideas to develop during one astronomers life to the other and how fast they improved with technology. 

Posted in Historical, Science | Tagged , , , , | Comments Off on Historical Astronomers in Context